四角形
四角形*しかっけい
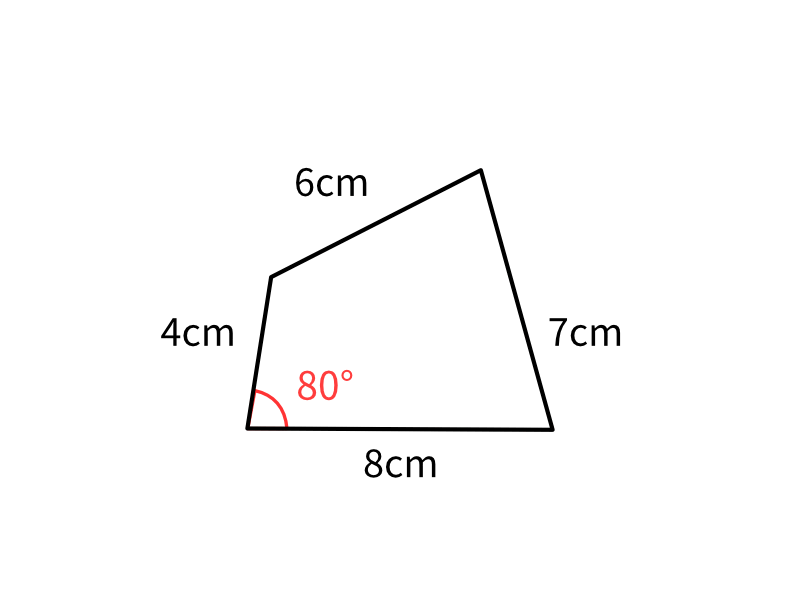
quadrilateral クアドリラテラルとは、4つの点とそれらを結ぶ 4つの線分で囲まれた平面図形のこと。
辺
辺*へんとは、四角形をつくるそれぞれの線のこと。
頂点
頂点*ちょうてんとは、となり合う2つの辺が交わる点*四角形の角のこと。
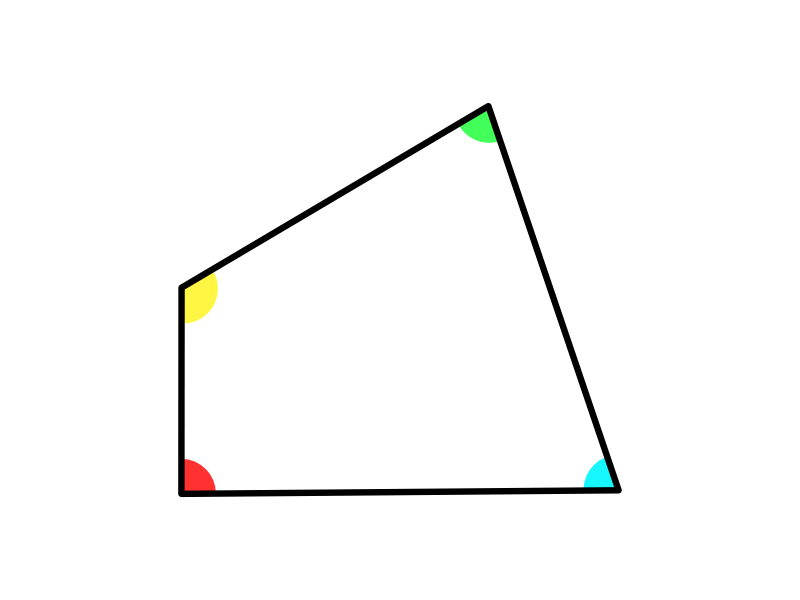
内角
内角*ないかくとは、各頂点から見て内側にできる角のこと。
外角
外角*がいかくとは、1つの辺ととなり合う辺の延長とがつくる角のこと。
辺*へんとは、四角形をつくるそれぞれの線のこと。
頂点
頂点*ちょうてんとは、となり合う2つの辺が交わる点*四角形の角のこと。
内角
内角*ないかくとは、各頂点から見て内側にできる角のこと。
外角
外角*がいかくとは、1つの辺ととなり合う辺の延長とがつくる角のこと。

対辺
対辺*たいへんとは、互いに向かい合った2つの辺のこと。
対角
対角*たいかくとは、互いに向かい合った2つの角のこと。
対角線
対角線*たいかくせんとは、四角形の隣り合わない2つの角*対角の頂点を結んだ線分のこと。
対辺*たいへんとは、互いに向かい合った2つの辺のこと。
対角
対角*たいかくとは、互いに向かい合った2つの角のこと。
対角線
対角線*たいかくせんとは、四角形の隣り合わない2つの角*対角の頂点を結んだ線分のこと。
四角形の内角の和
どんな四角形でも、四角形の内角の和は「360°」になる。
四角形の内角の和 1
四角形に 1つの対角線を引くと、2つの三角形に分けることができる。三角形の内角の和は「180°」になるので、2つの三角形の内角の和を足すと「180°+180°=360°」となり、四角形の内角の和は「360°」であると言える。
四角形に 1つの対角線を引くと、2つの三角形に分けることができる。三角形の内角の和は「180°」になるので、2つの三角形の内角の和を足すと「180°+180°=360°」となり、四角形の内角の和は「360°」であると言える。
四角形の内角の和 2
形や大きさがすべて同じ四角形を用意して、すべての内角を足すように並べてみると 1つの角に 4つの角がぴったり合わさる。円の角度は「360°」なので、四角形の内角の和は「360°」であると言える。
形や大きさがすべて同じ四角形を用意して、すべての内角を足すように並べてみると 1つの角に 4つの角がぴったり合わさる。円の角度は「360°」なので、四角形の内角の和は「360°」であると言える。
不等辺四角形
不等辺四角形
ふとうへんしかっけい
英語
US: trapezium トゥラピージアム
UK: irregular quadrilateral イレギュラー・クアドリラテラル
定義
物事の意味や内容をほかと区別できるように言葉で明確に限定すること。
・4つの辺の長さがすべて異なる四角形のこと。
定理
定義などから証明することができるもの。
ふとうへんしかっけい
英語
US: trapezium トゥラピージアム
UK: irregular quadrilateral イレギュラー・クアドリラテラル
定義
物事の意味や内容をほかと区別できるように言葉で明確に限定すること。
・4つの辺の長さがすべて異なる四角形のこと。
定理
定義などから証明することができるもの。
不等辺四角形の書き方